התיאוריה הכלכלית גורסת שמרבית בני האדם הן שונאי סיכון. במונחים פיננסיים משמעות הדבר שהם מעדיפים לקבל סכום כסף וודאי על פני קבלת סכום אי וודאי שהתוחלת שלו שווה לסכום הוודאי (בדוגמה פשטנית – מעדיפים לקבל 200 ₪ במקום להשתתף בהגרלה בה אפשר לזכות ב–100 ₪ בהסתברות של 50% וב–300 ₪ בהסתברות של 50%). כלומר פרט שונא סיכון יסכים להשתתף בהגרלה כזאת רק אם תוחלת הזכייה תעלה על 200 ₪, שהוא הסכום הבטוח (התוחלת השקולה לסכום הבטוח היא "שווה הערך הוודאי"). ההפרש שיביא לאדישות בין תוחלת תוצאת ההגרלה ובין הסכום הבטוח הוא פרמיית הסיכון הנדרשת.
שנאת סיכון ותשואה
באופן סכמתי חברה (פירמה) מממנת את פעילותה הכלכלית בשני מקורות הון – הון עצמי (קרי הון מניות) והון חיצוני (קרי אשראי). אם החברה נקלעת לקשיים בעלי החוב הם הראשונים בנשייה. לכן החזקה של אגרות חוב בטוחה יותר מאחזקת מניות, כי במקרה של פירוק החברה בעלי המניות יקבלו רק את היתרה השיורית, אחרי שהנושים (בעלי אגרות החוב) יקבלו את המגיע להם על פי חוזה ההלוואה. כתוצאה מכך תורת המימון גורסת שעקב שנאת הסיכון משקיעים ידרשו תשואה גבוהה יותר על מניות מאשר על אגרות חוב.
פרמיית הסיכון של החזקת מניות, אשר מכונה "פרמיית השוק", היא הפער בין תשואת מניות ובין תשואת נכס בטוח. אגרת חוב ממשלתית נחשבת לנכס בטוח. פרמיית השוק חשובה, היות שהיא משמשת מרכיב בחישובים דוגמת הערכת שווי של חברות. התשואה של אגרות חוב של חברות גבוהה מן התשואה של אגרות חוב ממשלתיות בגין הסיכון הגדול יותר הכרוך בהחזקתן.
השימוש בפרמיית השוק
פרמיית השוק משמשת בין היתר בהערכת שווי חברות. השיטה השכיחה להערכת חברות, שאומצה גם בפסיקה בישראל[2], היא של מודל היוון תזרים המזומנים (DCF – discounted cash flow). לפי מודל זה שווי החברה שווה לערך הנוכחי של תזרים המזומנים שהחברה צפויה להניב לאורך פרק זמן בלתי מוגבל, מהוון בשיעור תשואה. פרמיית השוק היא מרכיב בחישוב תשואת ההון העצמי של החברה. היא גם משמשת במודלים לבניית תיקי השקעות (asset allocation).
בהערכת חברות נהוג לבדוק את פער התשואה בין מניות ובין אגרות חוב ממשלתיות לתקופה של 10 שנים, היות שההערכות הן לטווחים ארוכים. אגרות החוב הממשלתיות נעדרות סיכון ביחס לפירעון (למרות העובדה שבהיסטוריה היו לא מעט מקרים בהם חוב ריבוני לא נפרע במלואו), אך לא ביחס לתנודתיות מחיר השוק עקב שינויים בשיעורי ריביות השוק לאורך זמן.
מקור הנתונים
בחנתי את פרמיית השוק בישראל במשך תקופה הארוכה ביותר עבורה יש נתונים – בשנים 2018-1980. עבור שנים אלו יש פרסום מסודר של הלשכה המרכזית לסטטיסטיקה (להלן – "הלמ"ס") של מדדי שיעור תשואה כולל ריאלי הן של מניות והן של אגרות חוב בשנתון הסטטיסטי לישראל. הלמ"ס התחילה למדוד את שיעור התשואה הכולל רק משנת 1977. עקב הסחרור האינפלציוני בו היה נתון המשק הישראלי בתחילת תקופת הבדיקה (בשנת 1996 נמדדה בפעם האחרונה אינפלציה דו ספרתית בישראל), עשיתי שימוש במדד שיעור התשואה הכולל הריאלי (בניכוי מדד המחירים לצרכן), כפי שהוא מפורסם על ידי הלמ"ס. במניות עשיתי שימוש במדד הכללי של המניות. באגרות חוב עשיתי שימוש בנתוני אגרות חוב ממשלתיות צמודות למדד המחירים לצרכן. כיום משקל אגרות החוב הלא צמודות משתווה למשקל אגרות החוב הצמודות למדד (ואף עולה עליו), אבל במרבית תקופת המדידה אגרות החוב הצמודות למדד היו דומיננטיות לחלוטין.
פרמיית השוק בישראל
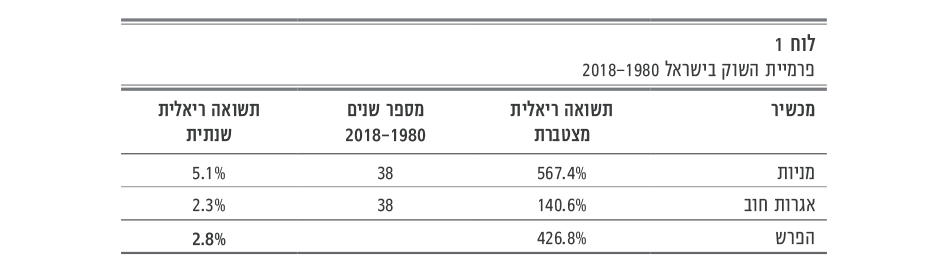
מן הבדיקה עולה שבחישוב של ממוצע גיאומטרי המניות הניבו תשואה שנתית ריאלית בשיעור 5.1% ואגרות החוב הממשלתיות בשיעור 2.3%, וההפרש עמד על 2.8%, כמוצג בלוח 1 להלן:
פרמיית השוק וויסות המניות הבנקאיות
תוצאה זו מעוותת על ידי ויסות המניות הבנקאיות והסדר המניות הבנקאיות שבא בעקבות הוויסות, שאירעו במהלך תקופה זו. המניות הבנקאיות לא שיקפו באותה תקופה כוחות שוק, ושעריהן נופחו כלפי מעלה על ידי הבנקים, כפי שהתברר במשפט הבנקאים[3] ובדו"ח ועדת החקירה לעניין ויסות מניות הבנקים (ועדת בייסקי). כשהוויסות נפסק, ירידת המחירים נבלמה בהתערבות הממשלה במסגרת הסדר מניות הבנקים. הלשכה המרכזית לסטטיסטיקה הכירה בכך ופרסמה עבור השנים 1992-1979 מדד מניות ללא בנקים מסחריים בשנתון הסטטיסטי לישראל.
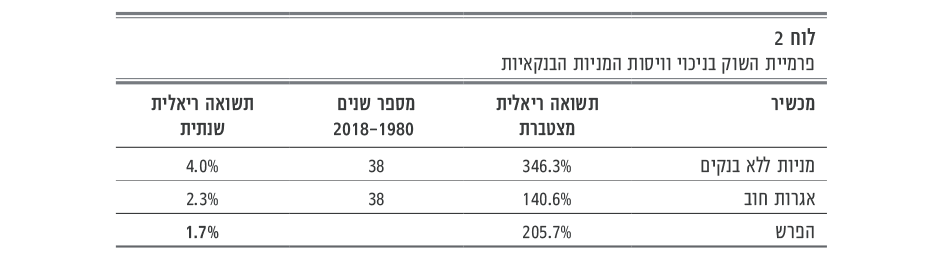
כאשר הצבתי עבור השנים 1992-1980 את המדד ללא בנקים מסחריים, תשואת המניות פחתה ל–4.0% ופרמיית השוק ל–1.7%, כמוצג בלוח 2 להלן:
ממוצע גיאומטרי או אריתמטי
התשואות השנתיות בלוחות 1 ו–2 חושבו לפי ממוצע גיאומטרי.
בספרות המימון קיימת מחלוקת מתודולוגית אם ראוי לחשב את פרמיית השוק לפי ממוצע גיאומטרי או אריתמטי.
Damodaran הציג את השיקולים בעד כל אחת מן החלופות[4].
במישור המתמטי הממוצע הגיאומטרי מניב תוצאות נמוכות יותר.
אם מניחים שהתשואות השנתיות אינן מתואמות והמטרה היא לחשב את פרמיית השוק לשנה בודדת, אזי הממוצע האריתמטי נחשב לנכון יותר.
במחקרים אמפיריים נמצא שיש מתאם סדרתי שלילי לאורך זמן, דבר המטה את הפרמיה כלפי מעלה.
ככל שהתקופה לגביה רוצים להסיק מסקנות על בסיס פרמיית השוק ארוכה יותר, ההצדקה לחישוב גיאומטרי גדלה.
Indro ו–Lee [5] הציעו לחשב ממוצע משוקלל של הממוצע הגיאומטרי והאריתמטי, כשהמשקל של הממוצע הגיאומטרי גדל ככל שפרק הזמן מתארך.
Damodaran מסכם את הדיון בכך שנימוק נוסף הוא שהממוצעים האריתמטיים הופכים לשיעורי היוון, אשר משמשים בחישובי היוון לאורך זמן ויש בכך חוסר עקביות.
בחישוב האריתמטי יש גם חשיבות לפרק זמן המדידה. העובדה שכדור הארץ מקיף את השמש במשך שנה לא משליכה על השווקים הפיננסיים. בניגוד לחקלאות, לפרק זמן של שנה אין משמעות מיוחדת במגזר הפיננסי.
להלן הנתונים המקבילים לפי חישוב של ממוצע אריתמטי:

מתקבלת פרמיית שוק בשיעור של 7.8%, מול 2.8% בחישוב גיאומטרי, הפרש של 5.0%.
גם כאן הגישה הנכונה היא של ניכוי השפעת וויסות מניות הבנקים:

כאן פרמיית השוק שווה ל–9.0%, מול 1.7% בחישוב גיאומטרי, הפרש של 7.3%.
למרות העובדה שהתשואה המצטברת ללא מניות הבנקים נמוכה ב–221% [6] (39% מתשואת המדד הכללי), פרמיית השוק גבוהה יותר. דבר זה נובע מכך ששונות התשואה השנתית של מדד המניות ללא בנקים הייתה גבוהה יותר.
הדבר מומחש בלוח 5 להלן בעזרת דוגמה פשוטה:
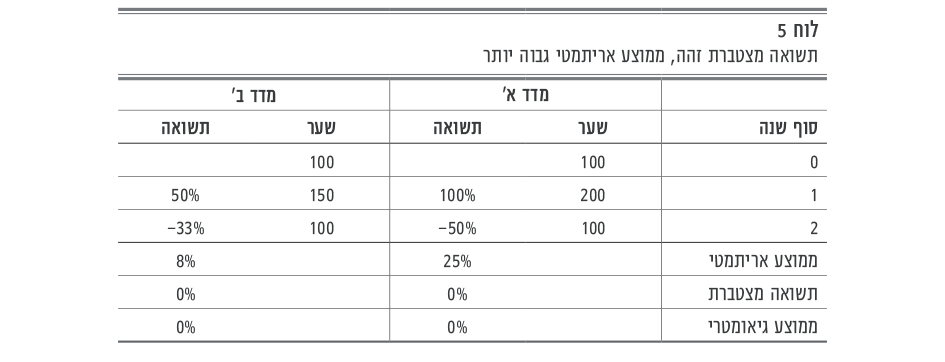
בדוגמה זאת יש שני מדדי ניירות ערך עם תשואה מצטברת של אפס. מדד א' תנודתי הרבה יותר ולכן התשואה הממוצעת בחישוב אריתמטי גבוהה יותר. הדבר נובע מן העובדה ששיעורי הירידה המאפסים את התשואה נמוכים יותר משיעורי העלייה, כי המכנה גדול יותר. כלומר – במדד א' תשואה חיובית בשיעור 100% מקוזזת בתשואה שלילית בשיעור 50%. במדד ב' תשואה חיובית בשיעור 50% "בלבד" מקוזזת בתשואה שלילית בשיעור 33% בלבד. סכום השינויים במדד א' הוא 50% ובמדד ב' 17%. לכן הממוצע האריתמטי של מדד א' גבוה יותר.
ברמה האינטואיטיבית פרמיית השוק הגבוהה יותר צריכה לפצות על הסיכון הגדול יותר של מדד א' לעומת ב'.
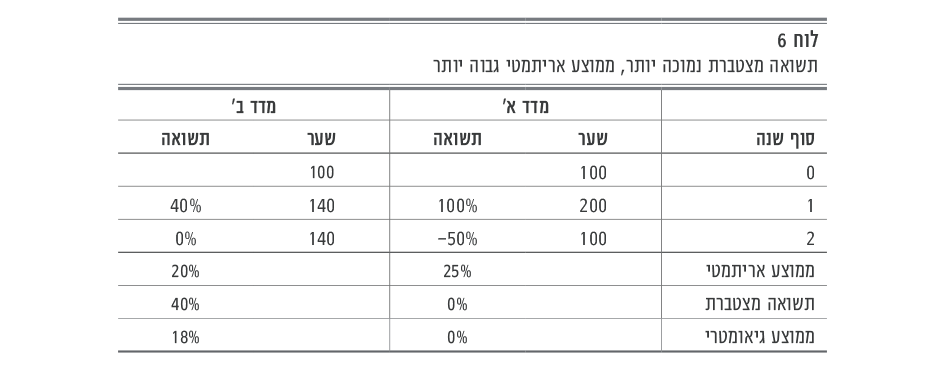
בלוח 6 להלן עוד דוגמה, בה למדד ב' תשואה מצטברת גבוהה יותר (40% מול 0%), אך התשואה השנתית הממוצעת בחישוב אריתמטי של מדד א' גבוהה יותר (25% מול 20%):
להלן ריכוז התוצאות של פרמיות השוק שהוצגו לעיל:

תדירות המדידה
בחישוב ממוצע אריתמטי התוצאה מושפעת מתדירות המדידה.
כפי שצוין לעיל, בשווקים הפיננסיים אין משמעות לתקופה של שנה, פרט לכך שנהוג למדוד הכול במונחים שנתיים. אם בני אדם יתיישבו על כוכב הלכת מאדים, בו השנה נמשכת 687 ימים, או על נוגה, שם השנה נמשכת 225 ימים, סביר שחישובי הריבית ימשיכו להיעשות לפי 365 ימים.
מסיבות של קונבנציה מקובל למדוד את הנתונים ברמה של שנה קלנדרית, אך אין לכך כל סיבה אמיתית. ניתן לצפות שככל שתקופת המדידה תתארך, אז התנודתיות המצטברת תגדל ולהיפך. כלומר אם תעשה מדידה חודשית, בדרך כלל התנודתיות במהלך חודש תהיה נמוכה מאשר במשך שנה. מצד שני אם יש תנודתיות בכיוונים שונים בתוך תקופת המדידה, אז ככל שהיא תתארך התנודות תתקזזנה ולכן התנודתיות תפחת עם התארכות התקופה.
להלן תוצאות הממוצעים האריתמטיים לתקופות מדידה שונות:
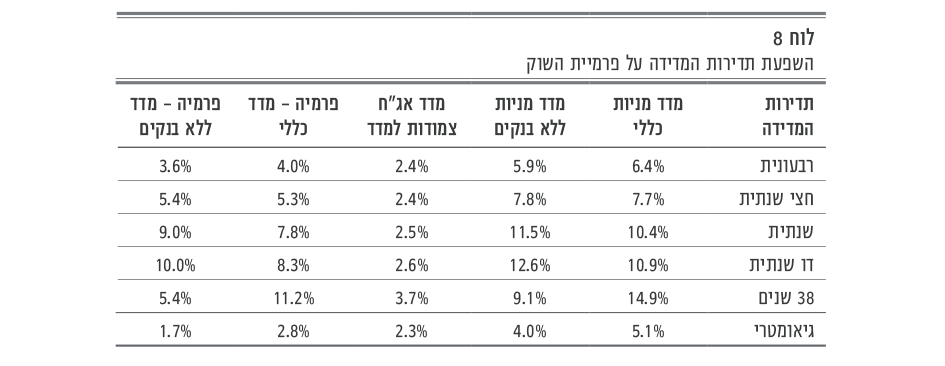
היות שהמדדים שהלמ"ס מפרסמת בשנתון הסטטיסטי לישראל הם שנתיים, בתדירות קצרה משנה התשואות נבנו בצורה סינטטית, כך שבתוך השנה שיעורי השינוי הוחזקו קבועים, בהיעדר נתונים מפורטים יותר. ברור שהדבר היטה את התנודתיות כלפי מטה.
כדי להציג את השפעת התדירות על בסיס נתונים אמפיריים בוצעה בדיקה מקבילה בהתייחס לנתוני המדד החודשיים שהלמ"ס מפרסמת בירחון הסטטיסטי לישראל. בנתונים החודשיים פורסם מדד מניות ללא מניות בנקים רק החל משנת 1984 (החל בירחון הסטטיסטי לישראל של חודש מאי 1984), כלומר אחרי סיום ויסות המניות. לכן החישובים מתייחסים רק למדד המניות הכללי. יצוין ששיעור התשואה בממוצע גיאומטרי שהתקבל היה נמוך ב–0.2% גם בהתייחס למניות וגם בהתייחס לאגרות החוב, כך שפרמיית הסיכון הייתה זהה – 2.8%.
להלן התוצאות שהתקבלו:
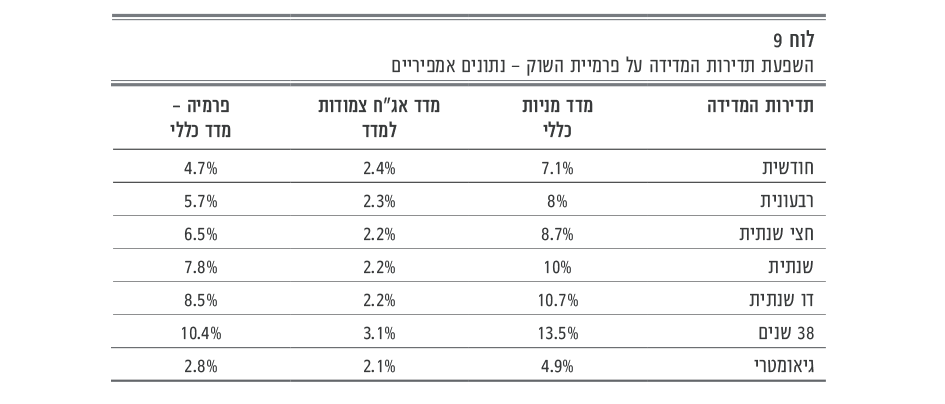
גם כאן הפרמיה מושפעת מתדירות המדידה בצורה מונוטונית – ככל שתדירות המדידה גדלה, הפרמיה פחתה.
עיתוי המדידה
חשוב להדגיש שיש חשיבות רבה לעיתוי המדידה.
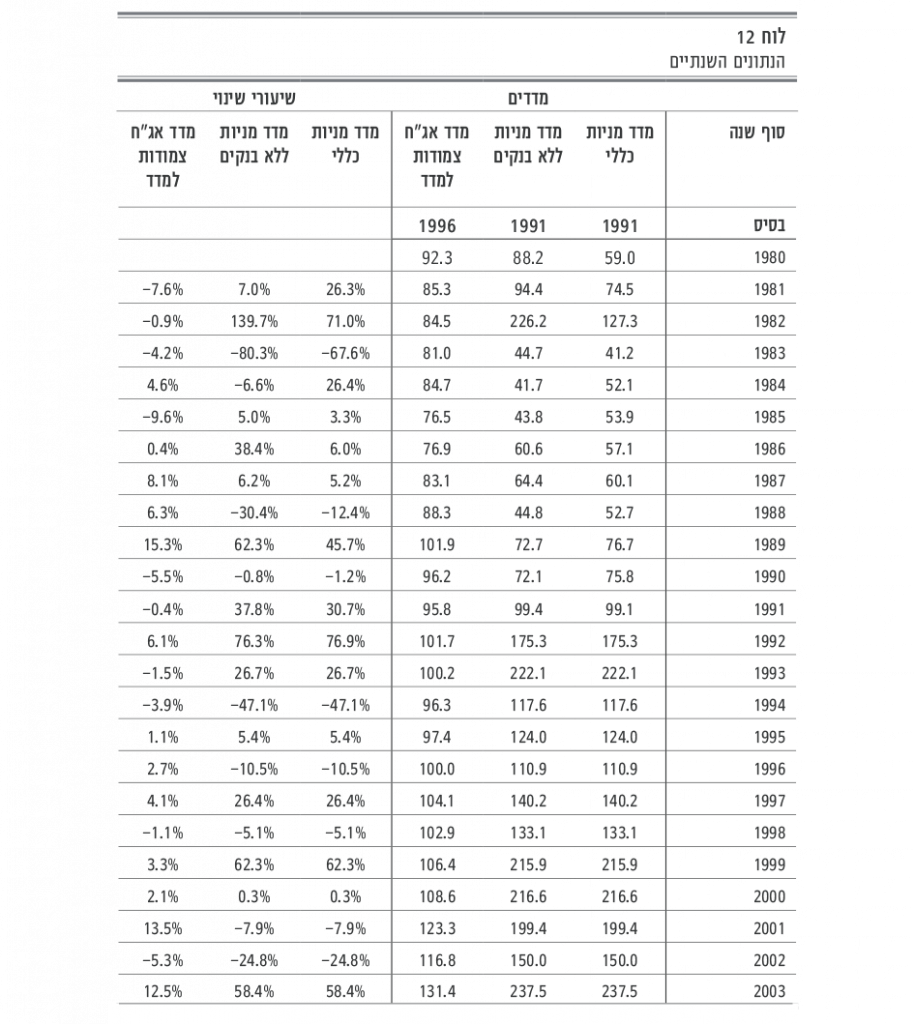
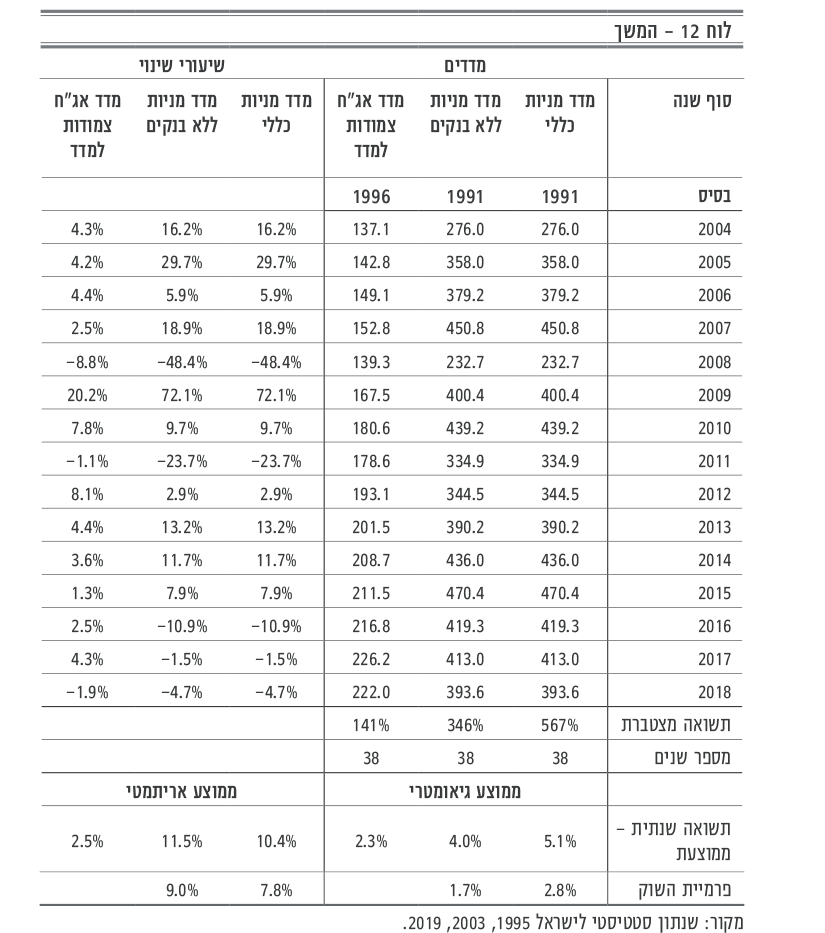
כפי שעולה מלוח 12 להלן, ב–1983 שוק המניות ספג הן את המפולת במניות הלא בנקאיות בתחילת השנה והן את משבר המניות הבנקאיות בסופה ובשנת 2008 אירע השפל הגדול (the great recession).
לו נקודת ההתחלה של הבדיקה הייתה סוף 1983, אחרי ירידות שערים בשיעור 68% של המדד הכללי ובשיעור 80% של המדד ללא מניות הבנקים, התוצאות היו שונות למדי.
כדי שהבדיקה תהיה ניטרלית ככל האפשר, נקודת ההתחלה שנבחרה היא הראשונה לגביה היה מידע זמין בנתוני הלמ"ס ונקודת הסיום נתוני 2018, האחרונים שהיו קיימים במועד הכתיבה. זוהי תקופת המדידה הארוכה ביותר שהייתה אפשרית בעת הזאת.
כדי להמחיש את ההשפעה המהותית של עיתוי המדידה, בלוחות 10 ו–11 להלן מוצגות הפרמיות בחישוב ממוצע גיאומטרי נע ל–10 ול–20 שנים בהתאמה:
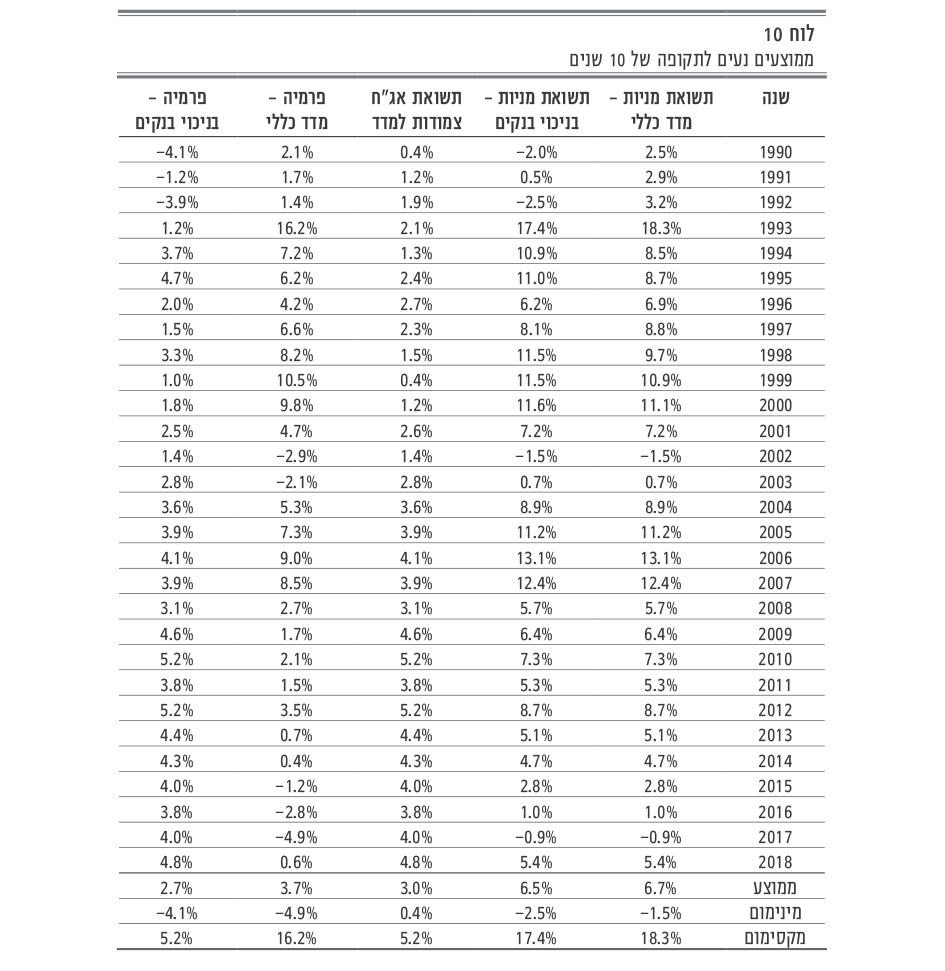
הממוצע על פני השנים חושב כממוצע אריתמטי.
ניכר הטווח הרחב מאד של הפרמיות עקב קוצר תקופת המדידה (10 שנים).
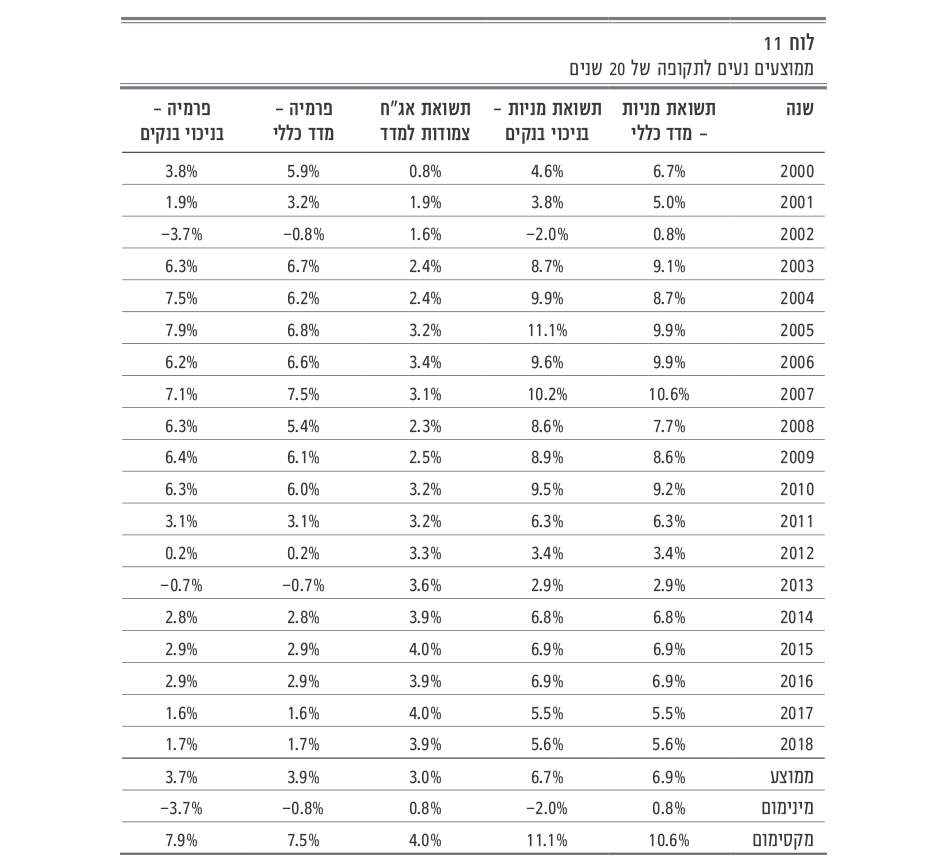
טווחי הזמן התקצרו כאן עקב הארכת תקופת המדידה ל–20 שנים (כלומר הנתון הראשון הוא רק עבור שנת 2000).
הכותב הוא עורך דין ושמאי מקרקעין, מוסמך לכלכלה, משפטים ומדיניות ציבורית.
[2] ע"א 779/06 קיטאל החזקות ופיתוח בינלאומי בע"מ ואח' נ' ממן ואח' (פורסם בנבו).
[3] ע"פ 2910/94 יפת ואח' נ' מדינת ישראל פ"ד נ (2) 221.
[4] Damodaran, Equity Risk Premiums (ERP): Determinants, Estimation and Implications – The 2015 Edition, pp. 27-28.
[5] Indro &Lee, Biases in Arithmetic and Geometric Averages as Estimates of Long-run Expected Returns and Risk Premium, Financial Management, v. 26, 81-90.
[6] 346% מול 567%.